Kristen Bieda, Alden J. Edson, Elizabeth Phillips, Michigan State University
The global “stay home” mandates to mitigate the spread of COVID-19 in early 2020 provided an unexpected opportunity to understand how much digital applications influence our daily lives. In some parts of our lives, we hardly needed to skip a beat - particularly advancements in video conferencing and online shopping helped make the situation considerably more bearable than what it might have been even five years earlier. Yet, we also discovered that one of the most vital institutions in the world - education - was very underprepared to continue on with “business as usual.” While we could keep attending our weekly yoga class via online streaming, teachers, students, and parents were scrambling to figure out how to realize learning from home. What the COVID-19 pandemic revealed was that, despite significant advances in recent years in videoconferencing technologies, existing digital learning technologies still fall short of helping teachers provide the kind of challenging, collaborative problem solving that is needed for all students to develop robust mathematical understanding.
Two of us are curriculum designers and work closely in the field with teachers on a regular basis to both design curriculum and support teachers’ work in enacting curriculum. Over the past three years, all of us have worked collaboratively with funding from the National Science Foundation on a digital platform for the Connected Mathematics Project (CMP) a research-based problem-centered curriculum widely used in middle schools around the world. When the pandemic forced school closings around the world, we were able to witness, through interviews with CMP teachers and reading posts on an online discussion board for CMP teacher leaders, how chaotic the shift was that teachers and students were experiencing. Some teachers were unable to keep using the CMP curriculum in any form. It took weeks for many schools to shift to remote learning, due to issues providing students access to adequate resources. Many teachers abandoned state or district standards and used a variety of strategies ranging from worksheets to puzzles to problem solving activities. Particularly early in the school shutdown, many teachers were humanely focusing more on checking in on students’ well-being than expecting them to complete assignments.
As months past for those schools who were trying to maintain an inquiry-based environment, we noticed the posts shift from “What are you doing?” to questions like “How are you helping students share their strategies?” While many teachers had limited time to meet synchronously with students, and other teachers knew that expecting all students to attend synchronous meetings was unrealistic, they were sharing strategies for how to deploy existing tools like Flipgrid (www.flipgrid.com) to help students learn collaboratively and foster, to a limited extent, some of the norms for mathematical communities that usually were the core of their work teaching CMP in face-to-face settings. As one teacher, Patricia, described: Well, what I've done is when we're in the Google meet, I will ask them to call on each other kind of a build-on thing, like if I were in class and said, pass the marker to the next person.
In many cases we were amazed at the creativity and amount of time CMP teachers were putting into the task of using CMP effectively in a remote learning environment. A common concern among teachers was that few, if any, digital tools could re-create the kind of responsive dialogue during problem solving, particularly when students work together in small groups, as Patricia explains: “Okay, so one thing that I think is hard to transport is the, the dialogue. Because like even with us right now, we can't have multiple groups going on at once, because it's only what the speaker is saying, it’s the only voice you hear in the moment.”
New Possibilities to Support Real-time Collaborative Work in the Digital Environment
Technologies such as Zoom for videoconferencing synchronously or Flipgrid for video-based collaboration are promising tools for creating a more collaborative environment in remote learning. However, all of these kinds of tools have shortcomings for supporting collaborative mathematical problem solving in that they are unable to provide students with the opportunity to not only see what others are doing during the problem-solving process but also use and modify each other’s work. Being able to share products, in real-time as students are problem solving, is key for promoting more equitable access for all students during the problem-solving process (Cohen & Lotan, 2014).
Through a partnership with Concord Consortium, funded by the National Science Foundation since 2017[1], we have been working to develop a digital platform for synchronous interactions that intentionally supports collaborative problem solving and promotes productive disciplinary engagement (Engle & Conant, 2002). As a digital curriculum, CMP problems involve three components in a contextualized, inquiry setting: (1) an Initial Challenge that contextualizes the problem and presents the challenge; (2) a What If…? that unpacks the embedded or encoded mathematics of the problem. Situations focus on what happens when you consider changed quantities or parameters, new aspects to the context, or different solution strategies; and (3) a Now What Do You Know? that connects learning to prior knowledge and provides focus on the learning goal of the problem.
To illustrate the nature of this new digital environment, we share an example of a CMP investigation where students build working definitions of similarity in mathematics terms (see Figure 1). The overall learning objective of the problem is to see how some similarity transformations, through changes in the x- and/or y-coordinate, move the figure and /or change the size around but preserve its shape or similarity. In the previous problem, students plot different Wump characters. Students plot characters Mug, Zug, Lug, Bug, and Glug when given different algebraic rules involving combinations of coefficients for x and y coordinates. Students are then tasked with the challenge of figuring out which family members are imposters, that is, which characters are not similar to Mug.
Problem 2.2
Hats Off to the Wumps: Changing a Figure’s Size and Location
Initial Challenge
Zack experiments with multiplying Mug’s coordinates by different whole numbers to make other characters. Marta asks her uncle how multiplying the coordinates by a decimal or adding numbers to or subtracting numbers from each coordinate will affect Mug’s shape. He gives her a sketch for a new shape (a hat for Mug) and some rules to investigate.
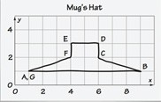
- Look closely at each rule and predict what will happen to the hat with each rule.
- Test each rule. How does your result compare with your prediction?
What If…?
Situation A. Writing New Hat Rules
What if you wanted to create a hat that is similar to Mug’s hat? What rule would you write if
- The side lengths are one third as long as Mug’s hat?
- The side lengths are 1.5 times as long as Mug’s hat?
- The hat is the same size as Mug’s hat but has moved right 1 unit and up 5 units:
- The image is in another quadrant:
Situation B. Negative Numbers and Rules
What if you multiply each coordinate by a negative number? What happens to the image?
Situation C. Isaiah’s Challenge: Putting the Hat on Mug
Isaiah challenges his group to write a rule that will put Mug’s hat on Mug. Is this possible? Why?
Now What Do You Know?
If you know the coordinate rules to create an image, how can you tell if the two figures are similar? How can you use the rule to predict the side lengths of the image? How is the effect of a coordinate rule like the effect of a rubber band stretcher or a copy machine setting?
Figure 1. CMP STEM Problem Format for Stretching and Shrinking Problem 2.2.
During the Launch, students make predictions about outcomes of the problem situation on their digital workspaces and verbally ask clarifying questions to each other. Launches focus on connecting to prior knowledge as well as presenting the challenge of the Problem (see Figure 2 for sample student work for this phase).
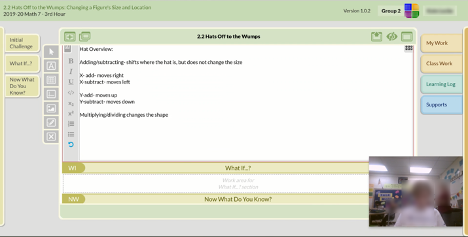
Figure 2. Examples of a Student Prediction.
During the Explore, students continue to work collaboratively in small groups to make sense of the problem. They gather data, share ideas, look for patterns, make conjectures, develop strategies, and create arguments to support their reasoning and solutions. Using Zoom breakout rooms can facilitate discussions during the explore. The key features that this digital environment provides is limitless access for students to see each other’s work in real-time and to click and drag work from other workspaces, incorporating copies of sections into their own workspace (see Figure 3).
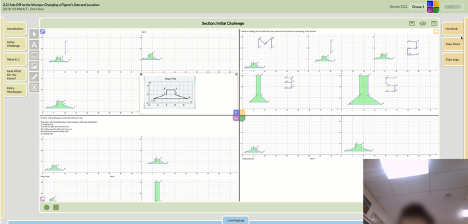
Figure 3. Sample Student Workspace Connected to Teammates.
Additionally, the platform has a teacher dashboard where teachers can observe students by circulating in the classroom or monitoring “live” student work on the digital platform via their tablet. For example, Figure 4 shows the teacher dashboard where the teacher can see “live” work from students in real-time. The teacher can also filter the dashboard by the three components of the CMP STEM Problem format and by “work-in-progress” or published work, navigating between views, showing the work by the class, a group view of four students, or an individual student.
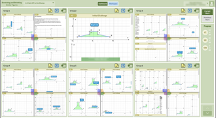
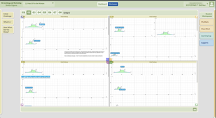
Figure 4. Teacher Dashboard and Teacher Digital Monitoring of One Group
During the Summarize phase, teachers and students share, discuss, and refine strategies and conjectures as a whole-class discussion. Teacher workspaces displayed to the class can incorporate student work along with new notes and work that can be shared to students. At the end of the Summarize phase, a teacher may choose to have students record some of their understandings in their Learning Log. Each entry of their Learning Log contains a workspace with all the same tools and features as other workspaces in the digital platform. Students can enter notes from the problem summary, key terms and definitions, important reflections or highlights of their work. For example, teachers often have students complete their Mathematical Reflections, which appears 3-4 times per unit, in the Learning Log (see Figure 5).
Mathematical Reflection
In this unit, we used proportional relationships to investigate similar figures or scale drawings, including how to determine if two figures are similar. In this Investigation,
What do you know about similarity?
How were proportional relationships used to study similarity?
Figure 5. Mathematical Reflection from the Stretching and Shrinking unit.
Imagining a More Resilient Curriculum for Shifts to Remote Learning
We argue that the digital platform we have developed offers some key affordances for collaborative mathematical problem solving in remote learning environments. Below, we outline these affordances and call on STEM curriculum designers and developers to consider how the kinds of tools we have developed for this platform could be incorporated in other STEM content areas.
Coherent Sequencing of Problems
During the COVID-19 pandemic, teachers grappled with important decisions about what content to teach in the limited time allocated for mathematics class. One way they make such decisions is to not only draw on their understanding of standards such as the Common Core State Standards for Mathematics (CCSSO & NGA, 2010), but they also need to: (1) recognize and understand the big mathematical ideas in the units (2) see the curriculum as a set of “connected” instructional units as opposed to a collection of activities (3) understand the way concepts are being developed and make connections to the way students learn mathematics.. In our work, we refer to developing students’ mathematical thinking over time as the Arc of Learning framework (Connected Mathematics Project, 2016). Rather than emphasizing student learning as practicing a set of isolated skills, the Arc of Learning framework consists of five phases that describes how understanding of big mathematical ideas are developed over time (Edson, Phillips, Slanger-Grant, & Stewart, 2019) and how particular problems are positioned within the underlying learning progressions of the curriculum materials over time (Edson, Gilbertson, Gonulates, Grant, Nimtz, Phillips, & Satyam, 2015). In the digital collaborative learning environment, the emphasis on student learning of mathematical understandings over time is evident in the Learning Log feature and the Mathematical Reflections questions that help connect learning between, within, and among mathematics problems.
Collaboration and Making Students’ Thinking Visible
In navigating synchronous learning environments, many CMP teachers faced difficult challenges of how to support student engagement and student-to-student interactions remotely in ways that were sensitive to students’ privacy and the demands of their learn-from-home situations. Our digital collaborative platform takes synchronous learning one step further, working in concert with tools such as Zoom to support face-to-face conversations while also helping students see both the product and process of each other’s problem solving. Thus far, our research investigating the quality of students’ collaboration with our digital platform in face-to-face settings shows that it can promote episodes of high productive disciplinary engagement (Bieda, Going, Kursav & Edson, 2020; Going, Kursav, Grant, Bieda & Edson, 2017). We argue that more attention should be paid in the development of educational technologies that focus more on how to support students’ interaction instead of teacher-centered tools focused on learning management.
Final Thoughts
In our work interviewing teachers and reviewing discussion board posts, we were especially struck by the persistence of teachers to maintain high standards for student learning using the CMP curriculum despite the likely strain they were experiencing in their own lives. They heroically took on the task and put in countless hours to figure out how to provide an accessible, yet powerful, learning experience. We read in their messages a lack of a strong infrastructure, not unlike what was seen with the system of public health in the U.S. and other countries particularly hard-hit by the pandemic, and a lack of access to remote curriculum resources for collaborative work that compounded the difficulty they faced in transitioning to remote learning. Our hope is that the difficulty and tragedy of the COVID pandemic prompts renewed and lasting interest in developing curriculum and collaborative digital platforms that can be resilient to shifts in where learning needs to happen.
References
Bieda, K., Going, T., Kursav, M., & Edson, A.J. (2020). Entailments of productive disciplinary engagement in technology-enhanced mathematics classrooms. Accepted paper for the 2020 American Education Research Association conference, San Francisco, CA. (Cancelled due to COVID-19 pandemic).
Cohen, E. G., & Lotan, R. A. (2014). Designing groupwork: Strategies for the heterogeneous classroom Third Edition. New York, NY: Teachers College Press.
Connected Mathematics Project. (2020, May 5). Arc of Learning Research Project. Retrieved from: https://connectedmath.msu.edu/research/ongoing-research/arc-of-learning…
Edson, A.J., Gilbertson, N.J., Gonulates, F., Grant, Y., Nimtz, J.L., Phillips, E., & Satyam, V.R. (2015). Studying the arc of learning in middle school mathematics curriculum materials. In T.G. Bartell, K.N. Bieda, R.T. Putnam, K. Bradfield, & H. Dominguez (Eds.), Proceedings of the 37th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 104-107). East Lansing, MI: Michigan State University.
Edson, A. J., Phillips, E., Slanger-Grant, Y., & Stewart, J. (2019). The Arc of Learning framework: An ergonomic resource for design and enactment of problem-based curriculum. International Journal of Educational Research. Retrieved from https://doi.org/10.1016/j.ijer.2018.09.020
Engle, R. A. & Conant, F. R. (2002). Guiding principles for fostering productive disciplinary engagement: Explaining an emergent argument in a community of learners’ classroom. Cognition and Instruction, 20(4), 399-483.
Going, T., Kursav, M., Slanger-Grant, Y., Bieda, K., & Edson, A.J. (2018). Understanding the nature of uncertainty in problem-solving situations. In Hodges, T.E., Roy, G. J., & Tyminski, A. M. (Eds.), Proceedings of the 40th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Greenville, SC: University of South Carolina & Clemson University
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Washington, DC: Authors.
[1] This work was supported by the National Science Foundation grants, DRL-1660926, DRL- 1620934, and DRL-1620874. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.


